ReLU 介绍

ReLU（Rectified Linear Unit）激活函数详解及意义

1. 数学表达式与特性

• 公式：

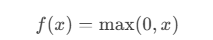
• 输出范围：[0,+∞)[0,+∞)，当输入 x>0x>0 时，输出为 xx；当 x≤0x≤0 时，输出为 0。

• 导数：

​

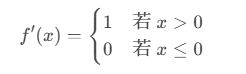
2. 核心优势

1. 计算高效

   • 仅需判断输入正负，无需复杂运算（如指数、对数），计算速度显著快于Sigmoid、Tanh等函数。

2. 缓解梯度消失

   • 在正区间梯度恒为1，避免了深层网络中因梯度连乘导致的指数级衰减问题（Sigmoid/Tanh的导数随输入增大趋近于0）。

3. 稀疏激活

   • 负输入被置零，仅部分神经元被激活，模拟生物神经元的“稀疏性”，减少参数冗余，增强模型泛化能力。

4. 加速收敛

   • 非饱和特性（正区间线性）使梯度保持稳定，反向传播效率高，大幅缩短训练时间。

3. 局限性及改进

1. 死亡ReLU问题（Dead ReLU）

   • 现象：若输入长期为负，梯度为0，导致神经元永久失活，无法更新参数。

   • 改进方案：

     • Leaky ReLU：负区间引入小斜率（如0.01），保留微弱梯度：f(x)=max⁡(αx,x)f(x)=max(αx,x)。

     • PReLU：将负区间的斜率 αα 设为可学习参数，自适应调整。

     • ELU：负区间使用指数函数平滑过渡，输出均值接近0：f(x)=max⁡(α(ex−1),x)f(x)=max(α(ex−1),x)。

2. 非零中心化输出

   • 输出均值大于0，可能导致参数更新方向偏移，但实际影响较小。

4. 应用场景

• 隐藏层默认选择：在CNN、全连接网络等结构中，ReLU是隐藏层的首选激活函数。

• 深层网络：有效缓解梯度消失，支持训练极深模型（如ResNet、Transformer）。

• 实时系统：计算高效，适合移动端或嵌入式设备部署。

5. 与其他激活函数的对比

6. 意义与影响

1. 推动深度学习革命

   • ReLU的引入解决了深层网络训练的梯度消失难题，使训练超深层网络（如ResNet-152）成为可能，推动计算机视觉、自然语言处理等领域的突破。

2. 计算效率与工程友好性

   • 相比传统激活函数，ReLU的计算速度和内存占用优势显著，支持大规模数据训练和实时推理。

3. 启发后续研究

   • ReLU的局限性催生了多种改进版本（如Swish、GELU），丰富了激活函数的设计思路，促进模型性能的持续提升。

7. 代码示例（PyTorch）

import torch
import torch.nn as nn

relu = nn.ReLU()
x = torch.tensor([-2.0, 0.5, 3.0])
y = relu(x)  # 输出：tensor([0.0000, 0.5000, 3.0000])

8. 总结

ReLU通过其简单性、高效性和对梯度消失问题的缓解，成为现代深度学习的基石之一。尽管存在死亡ReLU等问题，其改进版本和变种进一步扩展了其适用性。理解ReLU的工作原理及优化策略，对于设计高效、稳定的神经网络模型至关重要。